GPSでは現在地の位置情報を緯度および経度として取得することができますが、そこからある2点間の距離を求めるのは厳密にやろうとすると結構大変です。地表が球面であるのに加え、さらに厳密に言うとわずかに赤道方向に膨らんだ回転楕円体であるために複雑な計算が必要になります。厳密にやるには球面三角法や直交座標に変換する方法がありますが、これらの計算はかなり複雑でサーバー側のプログラムに組み込むには少々負荷が重くなってしまう問題があります。
ところがあまり細かいことを言わなければほぼ正確な距離を簡単な計算で求めることができるのです。これは別にどこで調べたわけでもなく自分で考えたものですが、おそらく少々数学のわかる方なら誰でも思いつく程度のものです。この方法では単純な三角関数だけで計算できますので、サーバー側で処理させてもほとんど負荷を与えません。その方法についてここで紹介しておきましょう。
前提として、この方法が適用できるのは、たとえばGPSのログに記録された各ポイント間の距離といったごく狭い範囲に限られます。経線の間隔は赤道から極に向かって収束していくため、当然ながら平行ではありません。しかし上に述べたようなごく小さい範囲で見れば平行とみなしても差し支えありません。実際、2万5千分の1地形図の図幅はどう見ても長方形にしか見えないでしょう。したがって経線の間隔が近似的に平行とみなせる場合に限ってこの方法が適用できます。緯度で言えば数分の範囲ならまったく問題ないと言えるでしょう。逆に東京~ロサンゼルス間の距離と方位を求めるような大きな範囲になると、当然ながら経線の間隔は平行とはみなせないため、この方法は適用できません。その場合は球面三角法を用いて計算する必要があります。
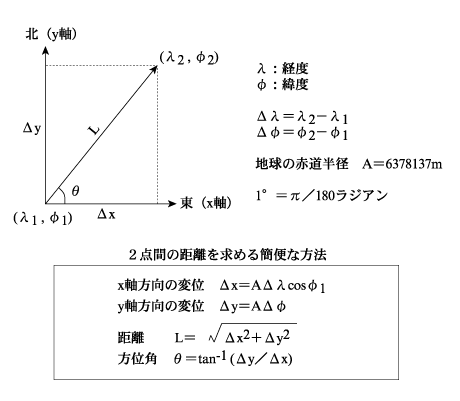
距離を求めたい2点の座標をそれぞれ(λ1,φ1), (λ2,φ2)とします。ここでλは経度、φは緯度を表します。また2点間の座標の変位を(Δλ, Δφ)とします。
まず、緯度方向の変位Δyについては地球を完全な球体と仮定すれば、緯度の変化に対する円弧の長さで簡単に計算できます。ここで地球の半径として赤道半径 A=6378137mを使用すると、Δy = AΔφとなります。なお言うまでもないことですが、角度は度ではなくラジアンに換算しなければなりません。1度=π/180ラジアンです。
一方、経度方向の変化Δx についても同様に経度の変化に対する円弧の長さで計算できますが、この場合、緯度によって円の半径が変化することを考えなければなりません。緯線に沿って地球をスライスしたとすると、その切り口の半径は緯度の余弦に比例します。したがって、Δx = AΔλcosφ1で求められます。ここで緯度の基準点としてφ1を採用しましたが、φ2をとっても実用上は同じことです。ほとんど意味はありませんが、もっと厳密にやりたければφ1とφ2の平均をとれば良いでしょう。
ΔxとΔyが求まれば、2点間の距離Lは三平方の定理により、それぞれの2乗の和の平方根で求められます。
また方位角θはΔy/Δxの逆正接で求めることができます。このとき方位角の基準は真東の方角を0度とします。
実際には地球は完全な球体ではないため、厳密に言うと誤差が生じますが、赤道半径と極半径の差は21km程度であるため、日本国内で使用する程度であればほとんど問題になりません。もう少し厳密にやりたいのなら、日本付近における地球の半径を回転楕円体モデルから計算すればできるはずです。厳密に計算した結果と比較してみると、緯度1分あたりの距離で誤差はせいぜい5~6m程度に過ぎませんでした。割合から言うと 0.3パーセント程度ですから、十分実用になる精度と言えるでしょう。
追記:JavaScriptのソースプログラムを提供しました。


コメント