今回は音楽理論を学ぶ上で最も基礎となる「音程」という考え方について解説します。少々耳慣れない言葉が出てきますが、これがわかってないと後々苦労することになりますので、正確に理解するようにして下さい。
普段鍵盤に馴染みのない人にはとっつきにくいかもしれませんが、鍵盤というのは音程というものを理解するのに非常に都合良くできています。したがって、ここでは鍵盤を使って説明します。鍵盤を演奏しない人もいったん鍵盤に置き換えて考えるクセを付けると理解しやすくなるかと思います。
音名
いろいろな音名
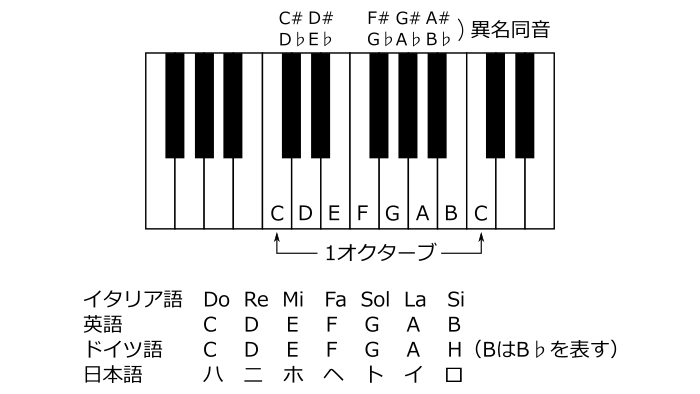
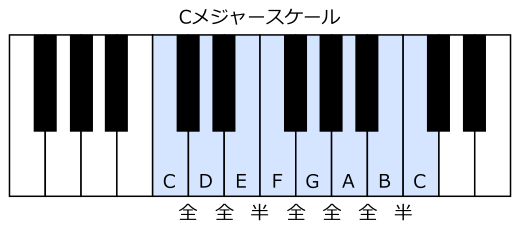
上の図はピアノの鍵盤を表したものです。白鍵上にはドレミファソラシの7音が順に並んでいて、もう一つ上がると1オクターブ上のドになります。つまり1オクターブの間には白鍵だけで7個の音が存在するわけです。
1オクターブ上がると音の周波数がちょうど2倍になるようにできています。
我々が日常的に使っているドレミ・・という音名は実はイタリア語読みで、言語によって様々な呼び方があります。ポピュラーミュージックの世界では英語読みが最も一般的であり、イタリア語読みとは次のように対応します。
ド→C
レ→D
ミ→E
ファ→F
ソ→G
ラ→A
シ→B
本講座でも英語読みを中心に使っていきますので、これはもういちいち置き換えなくても瞬時に出てくるように丸暗記してしまって下さい。
クラシックの世界ではドイツ語を用いることが多く、C(ツェー)D(デー)E(エー)F(エフ)G(ゲー)A(アー)H(ハー)という呼び方をします。ここでBの代わりにHとなっていることに注意して下さい。ドイツ語でB(ベー)と書いた場合にはB♭を意味します。余談ですが、オーケストラスコアでよく出てくる「クラリネットB管」などの表記は実はB♭管のことですので間違えないように気をつけて下さい。
また日本語ではドから順番にハニホヘトイロという音名を用います。主に学校の教科書や堅苦しい理論書で使われるあまり馴染みのない表現ですが、ハ長調、イ短調などの言葉は聞いたことがあるかと思います。
12音と平均律
1オクターブの間には白鍵7個のほかに黒鍵が5個あります。黒鍵は白鍵と白鍵の間にあり、両隣のちょうど中間の高さの音になります。したがって黒鍵も含めると1オクターブの間には全部で12個の音が存在します。これら12音すべてが等間隔になるように1オクターブを均等に12分割したものが平均律と呼ばれるものです。正確に言うと音の周波数の差が等しいのではなく、周波数の比がすべて等しいということです。ここで大事なことは、平均律ではすべての音が等間隔で配置されていますから、どの音から見ても音と音の間隔は同じであり、同等だということです。
臨時記号と異名同音
音名は全部で7つしかないため、黒鍵上の音は白鍵上の音が変化したものと考え、元の音に臨時記号を付けて表します。臨時記号にはいくつかの種類があり、元の音を半音上げたものが#(シャープ)、半音下げたものが♭(フラット)になります。また臨時記号で変化させた音を元に戻す場合には♮(ナチュラル)という記号を用います。
たとえばCを半音上げたものはC#になりますが、同時にDを半音下げたD♭も同じ音を指すことになります。このように呼び名が違っても同じ音を指す場合を異名同音と呼びます。どちらを使っても結果的には同じですが、後で説明する調性によって使い分けられます。
音程(インターバル)
音と音の隔たりのことを音程(インターバル)と呼びます。日常生活の中では「音程が高い・低い」などと音の高さを表す言葉として用いられることが多いですが、これは誤用であり、音楽理論では音程といえば音の高さのことではなく、音と音がどのくらい離れているかを表します。逆に音の高さは音高という言葉を用います。
基本的な音程の数え方
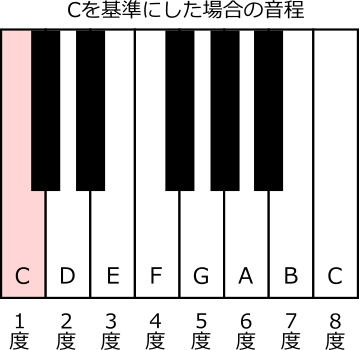
音程は度数という尺度で表現します。基本的には同じ音は1度と数え、白鍵上で隣接する音は2度、もう一つ隣の音は3度・・という風に順番に数えます。そして1オクターブ上の同じ音は8度となります。数学的に考えると同じ音は0度になりそうな気がしますが、音楽理論では1度と呼ぶことになっているのでそういうものと思って下さい。
12音すべての音程の数え方
しかし黒鍵上の音まで含めると音程の数え方はもう少し複雑になります。どの音を基準にするかによって当然異なりますが、ドを基準として音程を数えると下の図のようになります。
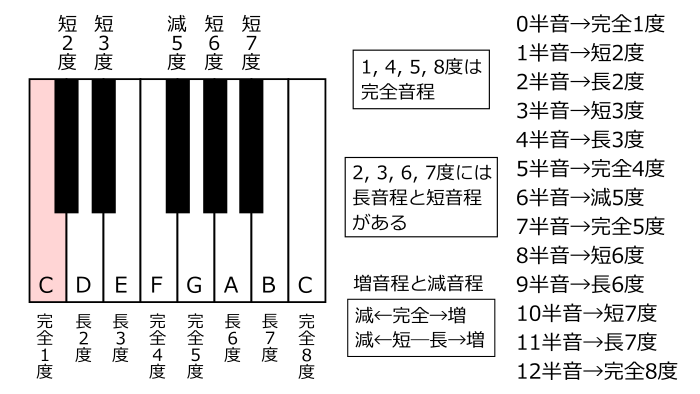
ここで度数の前に長、短、完全、減などの修飾が付いたことに注意して下さい。つまり黒鍵まで含めると全部で12音あるわけですから度数だけでは正確に表現できず、修飾が必要になるのです。
2度、3度、6度、7度の音には長短二つの音程が存在し、白鍵上の音はすべて長音程になります。また短音程はフラットが付いた音に相当します。
1度、4度、5度、8度の音は完全という修飾が付きますが、これは完全に響き合う音という意味です。楽器の音にはすべて倍音というものがあり、本来の周波数の2倍、3倍、4倍・・に当たる周波数の音を必ず含んでいます。倍音関係にある音は完全に響き合う性質があります。1度は当然として、8度は周波数が2倍ですからやはりきれいに響き合います。では5度はどうかというと、5度の音は周波数がちょうど1.5倍に当たりますので、1オクターブ上げると3倍になります。ですから1オクターブ上でやはりきれいに響き合うわけです。また転回のところで説明しますが、4度の音も1オクターブ下げると結局5度と同じになりますから、やはりきれいに響き合います。
増音程と減音程
完全音程あるいは長音程を半音広げたものを増音程といい、完全音程あるいは短音程を半音狭めたものを減音程といいます。ここではFとGの間にあるG♭が減5度となりますが、これは増4度と呼んでも同じことです。この講座では減5度で統一することにします。
半音と全音
1度を除いて最も短い音程は短2度ですが、これを特別に半音と呼びます。そして長2度、言い換えれば半音2つ分のことを全音と呼びます。
音程と半音の数
12音すべての音程は間に半音がいくつあるかで数えることができます。たとえば半音3個分は短3度であり、半音4個分は長3度となります。また半音5個分は完全4度、半音7個分は完全5度となります。半音6個分が減5度に相当することは特に重要ですから覚えておいて下さい。
音程の転回
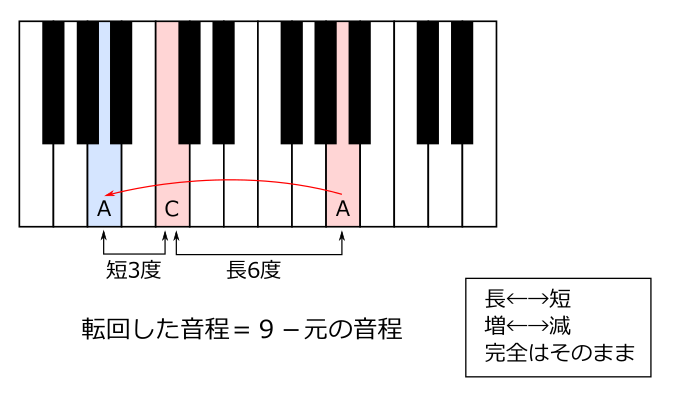
2つの音のうち一方を1オクターブ上げたり下げたりすることを転回と呼びます。転回しても同じ音ですから性質そのものは変わりません。また転回した音程の度数は9から元の音程を引いたものになります。さらに長音程は短音程に、短音程は長音程に、増音程は減音程に、減音程は増音程にそれぞれ入れ替わります。例外的に完全音程だけは転回しても名前が変わりません。
たとえばCとAの間の音程は上の図に示すように長6度ですが、A音を1オクターブ下げるとAとCの間の音程はいくらになるでしょうか? まず度数は上の公式にしたがって9から6を引けば3度となります。そして長音程は短音程に入れ替わるため、結果的に短3度の音程となります。したがって、長6度と短3度は同じ性質を持っていると言えます。
他にも長7度は短2度、完全4度は完全5度になるなど、音程というものは転回すると減5度を中心として左右対称の関係にありますから、実質的には半分しかないこともわかります。

コメント