FFTを行う際によく窓関数というものが用いられます。しかし何のために使うのかよくわからずに何となく使っている方も多いのではないでしょうか。後学のためにここで少しだけ説明しておきましょう。
まずその前にFFTを行う際の大前提について知っておかなければなりません。フーリエ変換の定義によれば、「あらゆる周期関数は正弦波と余弦波の重ね合わせで表すことができる」ことが知られています。ここで「周期関数」というところに深い意味があるのですが、要するに周期関数とはあるパターンが一定の周期で繰り返される関数のことを言うわけです。逆に言えば、フーリエ変換を行うためには周期関数でなければならないということになります。
しかしコンピュータでFFTを行う場合、無限のサンプルを取るわけにはいきませんから、当然ある限られた範囲のサンプルを取って変換を行うことになります。特にFFTの場合はサンプル数に制約があって、1024, 2048, 4096・・・といった2のべき乗個しかとることができません。たとえばサンプル数を4096に選んだとすると、音声信号を処理する場合、波形を4096個ずつのサンプルに区切ってFFTを行い、スペクトルに変換するわけです。ここで先の大前提と矛盾することにお気づきでしょうか？ 周期関数であるということは、先頭から4096サンプル取ったとすれば、その次の4096サンプルも、そのまた次の4096サンプルもまったく同じパターンを繰り返さなければならないことになります。もし音声の周波数が正確にわかっていて、その周期にピッタリ合わせて4096サンプル取ったとすれば、完全な周期関数にすることも理論上は可能でしょう。しかし現実には周波数があらかじめわかっていることはほとんどなく（そもそもFFTを行うのは周波数を求めるためです）、しかも周波数は時間とともに変化することが普通です。したがって一般的には有限のサンプル数で区切った波形が周期関数になっている可能性は限りなくゼロに近いのです。このことは下の図をご覧いただくとおわかりでしょう。サンプル数をNとした場合、Nサンプルごとに同じパターンが繰り返されれば周期関数になっていますが、一般にはそうなる可能性はほとんどなく、常に2)の状態になっています。
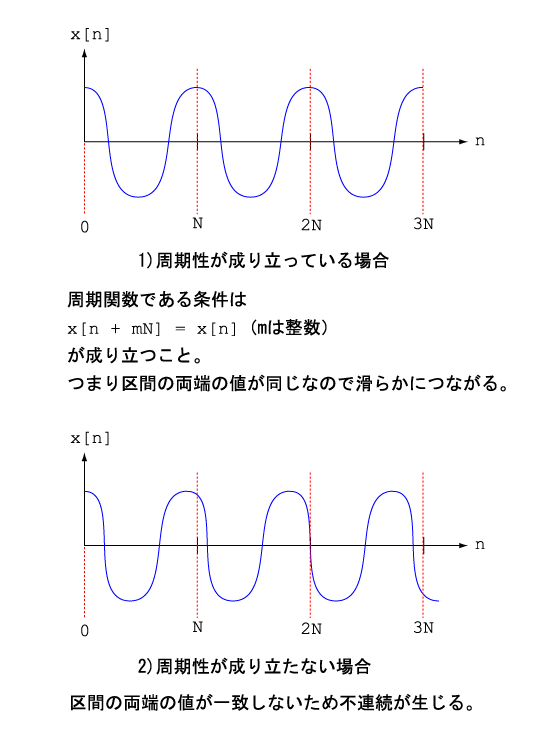
2)のように周期性が成り立たない状態でFFTを行うと何が問題になるのでしょうか？ 有限のNサンプルについてフーリエ変換を行う場合、そのNサンプルとまったく同じパターンが前後に永遠に繰り返されていることが前提になります。もし1)のように周期性が成り立っている場合、区間の初めと終わりの値が同じであることに注目して下さい。この場合、最初のNサンプルを永遠に繰り返していっても当然滑らかにつながります。しかし2)のように区間の両端の値が異なっていると、そのつなぎ目で不連続が生じてしまいます。もっと平たく言えば、波形が「カクカク」してしまうということですね。
一般に滑らかではない不連続性のある関数をフーリエ変換すると、そのスペクトルは低周波から高周波まで非常に広い範囲に分散します。たとえば矩形波のような不連続関数をフーリエ変換してみると、無限の高周波成分を含んでいることがわかりますし、もっと極端なデルタ関数のフーリエ変換はすべての周波数成分を均等に含むものになります。ですから不連続性のある波形をフーリエ変換すると、本来の周波数以外に「余分な」スペクトルがたくさん出てきて分解能が悪くなるということになるのです。
たとえば周波数が一定の正弦波をフーリエ変換したとします。もしその周波数に対応する周期がFFTのサンプリング周期と完璧に一致して周期関数になっていれば、スペクトルは1本しか立たないはずです。なぜなら正弦波は倍音成分を一切含まないからです。しかし周波数が少しでもずれていれば前述の理由により、本来の周波数以外に余分なスペクトルがいっぱい出てきてしまいます。これは実際にやってみればすぐわかります。この状態が下図に示す(A)の矩形窓に相当します。
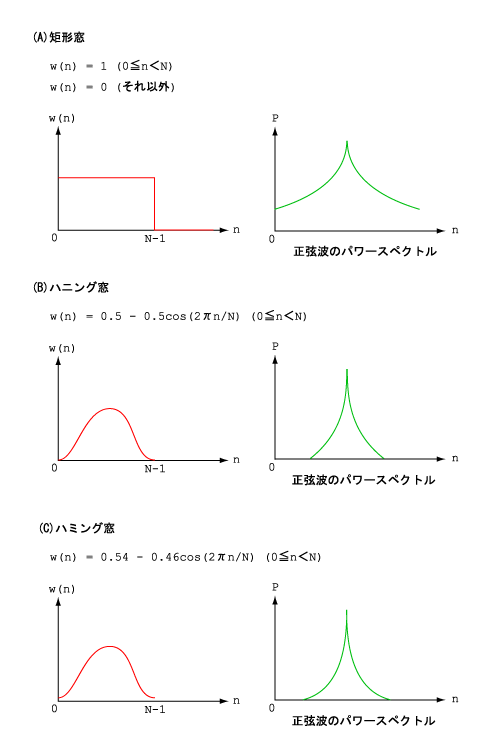
(A)矩形窓
これから窓関数について説明しますが、実は何もしなければ暗黙のうちに(A)の矩形窓を使っていることになるのです。定義から言うとサンプル要素nが0からN-1までの間は1で、それ以外はすべて0ということですが、要するに波形から単純にNサンプルずつ切り出すことと等価です。この場合、区間の両端における不連続性については何も考慮されていませんから、正弦波をフーリエ変換したとしても図のようにスペクトルは大きく広がったものになってしまいます。
そこでこの不連続性をできるだけ目立たなくするために「本来の」窓関数というものを使うわけです。一般に窓関数w(n)は次式のように波形x(n)に掛け合わせることによって使用します。
f(n) = w(n) x(n)
そしてこのf(n)をフーリエ変換することによって所望の結果を得るわけです。
窓関数については多くの学者によってたくさん考案されていますが、特に簡単かつ実用性の高いものとして次の2つを紹介しておきます。
(B)ハニング窓
これはハンという人によって考案されたので「ハン窓」と呼ぶこともありますが、次のハミング窓と語呂がよいことからハニング窓と呼ばれることが多いようです。定義は図の(B)に示されています。この窓関数の特徴は区間の端に向かってなだらかに小さくなっていき、両端は必ずゼロになるということです。ゼロになるわけですから、元の波形がどんなに不連続であっても両端の値は必ずゼロで滑らかにつながるわけですね。なおnはN-1までだから右端でゼロにならないじゃないかと思われる方がいるかもしれませんが、これは離散化しているためであり、連続量つまりNを無限大にした極限では0になることがおわかりでしょう。
ハニング窓を適用して正弦波をフーリエ変換した場合のスペクトルは、矩形窓を使う場合に比べて「ノイズフロア」が小さくなり、ピークがはっきりと現れるようになります。
(C)ハミング窓
これはハニング窓を改良したもので、形はまったく同じですが、両端がゼロにならないところが特徴です。したがって不連続性がわずかながら残っているわけです。両端を完全にゼロにしてしまうと区間の両端でのふるまいが無視されてしまうため、それを防ぐためにこのようにしたのでしょう。
ハミング窓を適用して正弦波をフーリエ変換した場合のスペクトルは、ハニング窓を使った場合とよく似ていますが、不連続性が若干残っている分、裾野の広がりはわずかに大きくなります。その代わりピークはより鋭くなって、周波数分解能が高まるという特徴を持っています。
以上、代表的な窓関数について説明しましたが、実際はもっと多くの窓関数が存在して用途に応じて使い分けられます。しかし音声処理でFFTを行う場合の主な目的はスペクトル解析や周波数推定（採譜）ですから、特にハミング窓について知っておけばほぼ十分であるともいえるでしょう。