FFTの扱い方

音声処理を扱うプログラムで非常によく用いられるものにFFT（高速フーリエ変換）があります。これは従来非常に時間のかかる計算であったフーリエ変換のアルゴリズムを改良して飛躍的に高速化したものですが、こういうものはすでに優秀なライブラリがいくらでも提供されていますので、その仕組みまで知る必要はありません。プログラマーとしては単にライブラリを呼び出して結果を得られればよいだけのことです。

音声処理でFFTを行う目的としては、時間の関数である波形を周波数の関数であるスペクトルに変換するために主に用いられます。つまりどの周波数の音がどのくらいの割合で含まれているか（スペクトル）を求めるときに使うわけです。ところが実際にFFTのライブラリを使おうとするとどうやって入力を与え、出力を得ればよいのか悩んでしまうことがあります。それは複素数という厄介なものが登場するからですが、特に数学の苦手な方にとってはそれだけでアレルギー反応を起こしてしまうようです。

本来、複素数というものは高校数学あたりで習っているはずなのですが、理系の大学に進んだ人以外、たいがい忘れているようです。ここで複素数についてもう一度復習しておきましょう。

複素数というものは一般に実部と虚部に分けて考えることができます。任意の複素数をxとすると、

x = a + b i

という形に表すことができます。ここでaを実部、bを虚部といいます。そして i は虚数単位と呼ばれ、2乗すると-1になるという変な性質を持っています。つまり i × i = -1です。

もう少し話を具体化して音声信号を扱うことにすると、一定時間ごとにサンプリングされた音声信号、すなわち波形x[n]は

x[n] = a[n] + b[n] i

という形に離散化して表すことができます。プログラムではこれを配列として扱うことはおわかりですね。

さてこの波形x[n]をフーリエ変換する場合、どうすればよいのでしょうか？　通常FFTのライブラリは入力・出力ともに複素数になっています。つまり実部と虚部の2組の配列を渡すか、または独自に定義された複素数型を使って受け渡しを行います。同様に結果も複素数として返ってきます。ところが、初めての人はまずここで悩んでしまうのではないでしょうか？

実は波形を入力として渡す場合は完全な実数と考えられますので、実部のa[n]だけを渡せば十分です。つまり虚部b[n]はすべて0とします。そしてFFTの関数を呼び出せばよいわけです。

厄介なのは出力の方です。実数である波形をフーリエ変換した結果は一般的に複素数になります。やりたいことは周波数のスペクトルを求められればよいのですが、この複素数をどのようにして扱えばよいのか途方に暮れてしまうことでしょう。

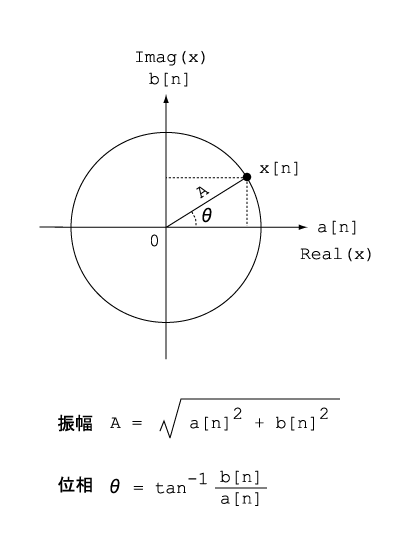
複素数というものは一般に上の図のような複素平面を用いて表します。任意の複素数x[n]は、実部a[n]を横軸、虚部b[n]を縦軸とする直交座標上の一点として表すことができます。ここで少し見方を変えて実部・虚部という表現から振幅と位相という表現に置き換えることを考えます。これは要するに直交座標から極座標への変換と同じです。振幅Aは三平方の定理によりa[n]およびb[n]の2乗の和の平方根をとったものになることはおわかりでしょう。同様に位相θは簡単な三角関数でb[n]/a[n]の逆正接で求められます。

ここでスペクトルを求める場合に重要なのは振幅の方です。位相スペクトルというものもあるのですが、人間の聴覚にとっては振幅スペクトルが大きな意味を持つので、通常は振幅スペクトルだけを考えれば十分です。ですからFFTを行って得られた結果から、上の式にしたがって振幅Aを求めてやればよいということになります。これが普通に音のスペクトルと呼んでいるものです。

なお振幅とよく似たものにパワー（電力）があります。一般にパワーPは振幅の2乗に比例しますので、

P = A × A

すなわちAの2乗がパワーになります。パワースペクトルという呼び方をすることもありますが、その場合は振幅の2乗の分布を表していると考えればよいでしょう。上の式で振幅Aを2乗すると平方根が取れますから、単にa[n]の2乗とb[n]の2乗の和になります。

またスペクトルはよく対数を取ってデシベルで表すことが多いですが、振幅（電圧）とパワー（電力）で定義が少し異なります。すなわち

振幅の場合　　dB = 20log A
パワーの場合　dB = 10log P

のように前の係数が2倍だけ異なります。これはよく考えるとPはAの2乗ですから、対数を取るとそれが2倍になって前に出てくると考えれば理解できます。

次にフーリエ変換した結果の周波数はどうやって求めればよいのでしょうか。FFTの制約により、ポイント数は1024, 2048, 4096･･･といった2のべき乗しかとることができませんが、FFTを行った結果はこれらの要素数をもった配列になっているわけで、それぞれの配列要素が表す周波数を知りたいわけです。

FFTのポイント数をN、サンプリング周波数をfsとしたとき、n番目の配列要素（もちろんnは0からN-1まで）に対応する周波数f[n]は次の式で求めることができます。

ここでn = Nを代入してやればfsに等しくなりますから、感覚として理解できるでしょう。つまりFFTを行って得られる結果の周波数範囲は0からfs（離散化しているので実際は一つ分少ない）までになります。ところがこれがすべて有効というわけではありません。よく知られているようにサンプリング周波数がfsであるとき、離散化して表現可能である周波数の上限はfs/2に限られます。これをナイキストの定理といい、fs/2のことをナイキスト周波数と呼んだりします。一般にFFTを行って得られるパワースペクトルは下図に示すようにナイキスト周波数を境にして左右対称になります。

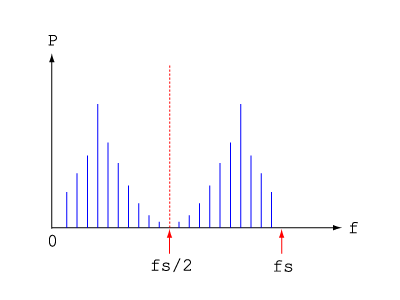
つまり右半分は左半分の虚像であって意味はないということですね。したがってFFTの結果で実際に有効なのはn = 0　～ N/2 – 1までの配列要素ということになります。

最後に具体的なイメージを持ってもらうために、実際に音声処理でよく使われる数値を代入してみましょう。まずサンプリング周波数fsはCDと同じ44100Hzが最もよく用いられますね。そしてFFTのポイント数ですが、これは多ければ多いほど周波数分解能が上がることは上の式からわかりますが、逆にサンプル時間を長く取る必要があるため、時間分解能は低下してしまいます。目的によっても異なりますが、一般的には両方の兼ね合いから4096くらいを選ぶことが多いようです。その場合の周波数分解能は

44100Hz / 4096 = 10.7Hz

ということになります。もちろんナイキスト周波数はｆｓの1/2で22050Hzですね。したがってこのケースでは、n番目の配列要素に対応する周波数f[n]は

f[n] = 10.7 × n　(Hz)

ということになり、FFTの結果が有効な上限周波数は

10.7Hz × (2048 – 1) = 21903Hz

ということになります。